ICML 2020
So the International Conference on Machine Learning (ICML) just ended and it was overall a great experience for me.
My favorite talks
This blog post will aim at presenting some of the talks I really enjoyed watching. They are more or less in my order of preference. Clicking on the title will take you to the ICML website for which you need a registration. The link to the paper is accessible regardless.
. Black-Box Variational Inference as a Parametric Approximation to Langevin Dynamics Matt Hoffman, Yian Ma [paper]
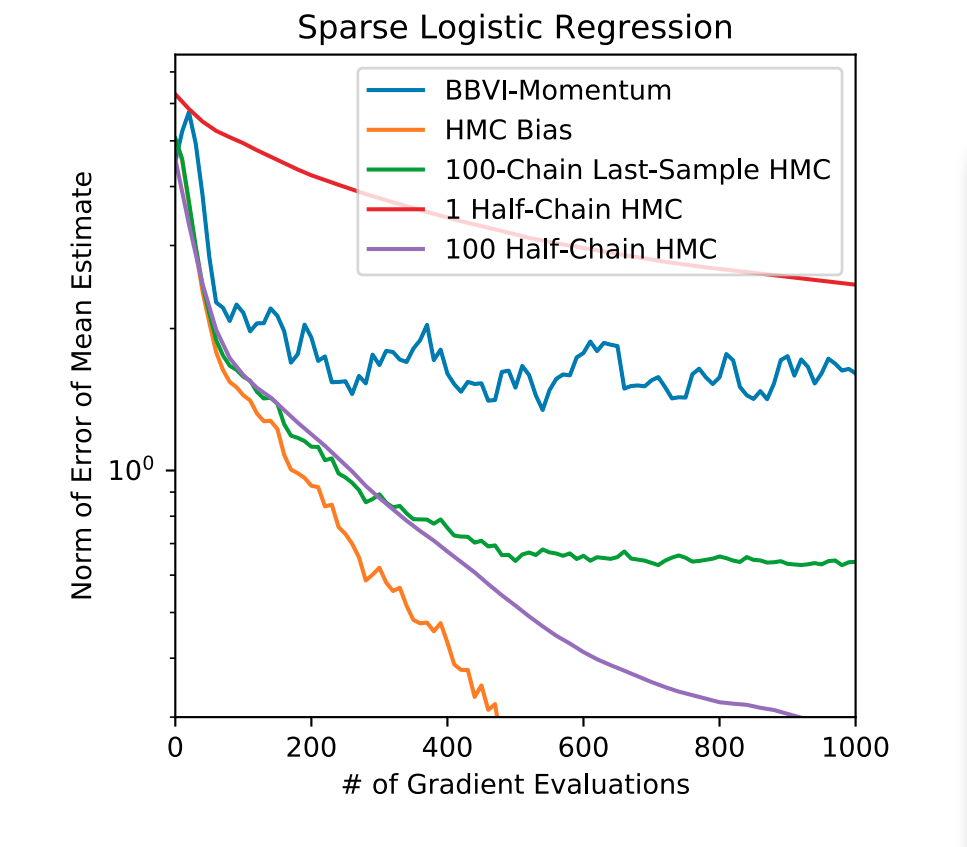
Matt Hoffman strikes again! This work is more about a high-level understanding of the difference between variational inference (VI) and Langevin dynamics. Two topics I am highly interested in.
Here is what I got from it: The general consensus is that sampling methods (like the Metropolis Adjusted Langevin Algorithm) are less biased then VI methods like Black-Box Variational Inference (BBVI) since they converge to the true target distribution and are not limited to some parametrization. However VI methods have faster convergence and it is easier to assess that they have reached their optima.
What Hoffman and Ma shows, is that the dynamics of both methods, which are essentially relying on sampling (one for estimating the distribution and one for estimating its gradients) or extremely similar. This kind of results appear more and more in recent papers like the paper Stochastic Gradient and Langevin Processes from the same conference.
Based on this equivalence they show that MALA can be interpreted as some kind of non-parametric BBVI. And that if one does not wait for the convergence of the sampler, decent results can be obtained already. It turns out that for some cases that these results are better or equal than the ones of BBVI. This is definitely thought-provoking! Finally, they argue that with parallelization it is now easier to run multiple chains and that this can help to outperform VI approaches.
I really recommend watching the talk as on top of the interesting work, Matt Hoffman is an amazing speaker!
2. All in the (Exponential) Family: Information Geometry and Thermodynamic Variational Inference Rob Brekelmans, Vaden Masrani, Frank Wood, Greg Ver Steeg, Aram Galstyan [paper]
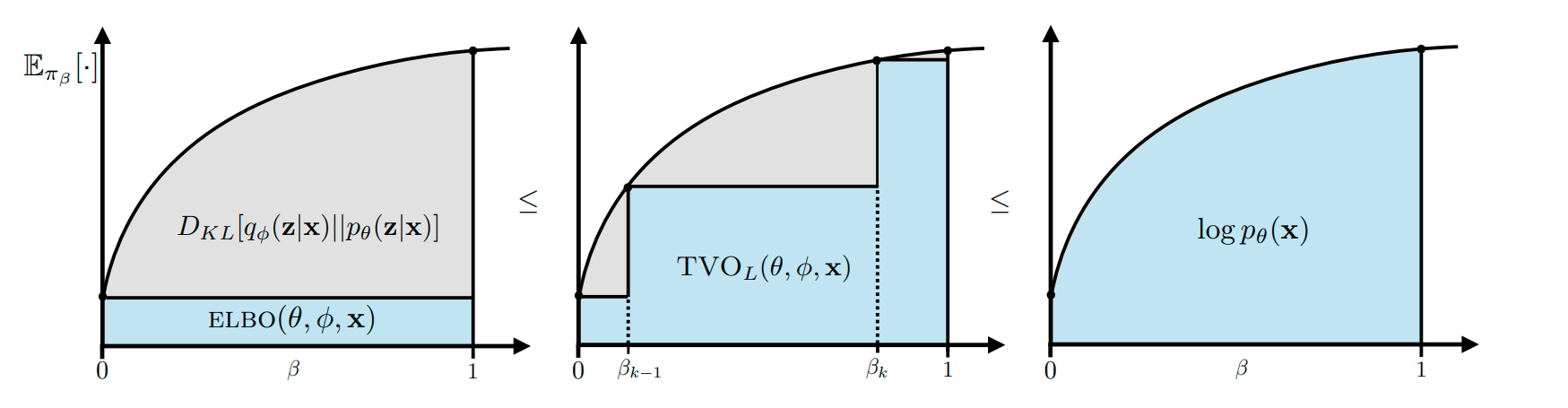
This paper is based on the Thermodynamic Variational Objective paper which have yet to read! But the general idea it that we replace the ELBO by a series of "tempered" ELBO, where the variational distribution is a mixture between a variational family and the joint distribution .
By progressively going from to we go from the variational distribution to the true posterior. This gives us a much more exact estimate of the log-evidence. For those interested in this approach there is this blog post but I will probably try to write my own.
Now one normally integrate over a couple of but they show that by choosing the right one can already improve the ELBO value. To do this they rewrite as an exponential family :
To be honest I am not sure how this works for :slightlysmilingface:
They also show that one can when integrating from to , one can automatically find the best step-size.
From the discussions one of the pit-falls of the methods seems to be the dimensionality of the problem. The expectations computed require importance sampling, which is known to be weak in high-dimensions.
3. Involutive MCMC: One Way to Derive Them All Kirill Neklyudov, Max Welling, Evgenii Egorov, Dmitry Vetrov, [paper]
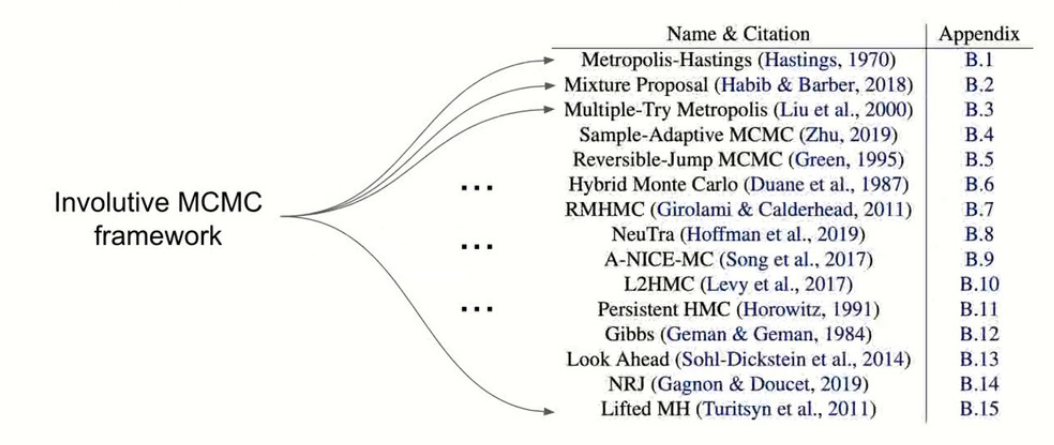
Generalization papers are always interesting because they bring a higher level of what some algorithms do. In this talk they aim at bringing a lot of Markov Chain Monte Carlo (MCMC) algorithms under one hood.
The basic idea of MCMC is to sample from a distribution by moving in the variable domain. Every move is subject to a rejection step, based on probability of the sample and the probability of the move. The samples collected will then be assumed to come from the target distribution. More formally the chain is
where the condition is that the kernel is density invariant :
One such kernel is where has to respect the condition
When adding the acceptance step one gets the following kernel
Now the problem with getting a satisfying this condition is that you will end up cycling between two locations. To solve this problem we need an additional auxiliary variable .
The involution restriction is now relaxed to . If we take the Metropolis Hasting algorithm this would be sample our proposal. For example for the random walk algorithm, this would mean sampling from a Gaussian centered in . Then (notice the permutation). The acceptance rate gives then
Following this definition, they list a series of tricks including additional auxiliary augmentations, additional involutions and deterministic map.
This talk really fascinated me as it really gives openings to create new and more efficient sampling algorithms!
Other talks
Here are other presentations that really caught my attention and that I will probably explore later
Scalable Exact Inference in Multi-Output Gaussian Processes Wessel Bruinsma, Eric Perim Martins, William Tebbutt, Scott Hosking, Arno Solin, Richard E Turner [paper]
General framework for multi-output GPs with a smart projection to reduce the complexity of the problem. It looks very sound theoretically
Sparse Gaussian Processes with Spherical Harmonic Features https://icml.cc/virtual/2020/poster/5898[paper]
Augmenting the data with an additional parameter (same for all data) and then projecting the data on an hypersphere to use spherical harmonics as inducing points
Efficiently sampling functions from Gaussian process posteriors James Wilson, Slava Borovitskiy, Alexander Terenin, Peter Mostowsky, Marc Deisenroth [paper]
By separating the contribution of the prior and the data, one can sample more efficiently (linear time!) by using random fourier features for the prior.
Automatic Reparameterisation of Probabilistic Programs Maria Gorinova, Dave Moore, Matt Hoffman [paper]
By creating an interpolation between the centered version and non-centered version of a graphical model one can find the optimal representation for sampling/inference.
Stochastic Differential Equations with Variational Wishart Diffusions Martin Jørgensen, Marc Deisenroth, Hugh Salimbeni [paper]
When one wants to represent noise with a non-stationary full covariance depending on time a Wishart process helps to determine it. The technique use GPs for the cholesky parameters and present a low-rank approximation for efficiency
Stochastic Gradient and Langevin Processes Xiang Cheng, Dong Yin, Peter Bartlett, Michael Jordan [paper]
Show equivalence between Stochastic Gradient Descent (SGD) and Langeving processes (them again!)
Variance Reduction and Quasi-Newton for Particle-Based Variational Inference Michael Zhu, Chang Liu, Jun Zhu [paper]
Preconditioners for optimization are not straight forward in the particle-based optimization framework. This work aims at solving that
Learning the Stein Discrepancy for Training and Evaluating Energy-Based Models without Sampling Will Grathwohl, Kuan-Chieh Wang, Jörn Jacobsen, David Duvenaud, Richard Zemel [paper]
Stein Discrepancy is complicated to use, and the kernelized versions has a lot of flaws, instead they propose to learn a constrained neural net to replace the kernel and obtain better results
Non-convex Learning via Replica Exchange Stochastic Gradient MCMC Wei Deng, Qi Feng, Liyao Gao, Faming Liang, Guang Lin [paper]
One runs two processes with very different stepsize, there is then a chance for the sampler to switch between the two chains, allowing for a compromise between exploration and exploitation.
Handling the Positive-Definite Constraint in the Bayesian Learning Rule Wu Lin, Mark Schmidt, Emti Khan [paper]
In order to optimize a positive-definite matrix, they propose to add a corrective term (through information geometry) to ensure the PD constraint is kept.
The online format
Due to COVID the conference was naturally online, which was for me a double-edged sword. On one hand it is amazing to be able to parse the presentations one by one and to take time to understand each topic. On the other hand, the lack of physical presence made it quasi-impossible to network with other people.
I went to a few poster sessions, aka local Zoom meetings, and it was definitely a slightly awkward experience. You suddenly end up in front of the multiple authors. It definitely puts a lot more pressure. If there is one point that needs to be improved it is this one!